Schärfentiefe konventionell und ultimativ berechnet

Wie war das noch im Physikunterricht? Eine sphärische Linse - also eine Linse mit kugelförmiger Oberfläche - bündelt alle Lichtstrahlen, die von einem Punkt ausgehen, in einem "Bildpunkt".  So sollte es in einer idealen Welt sein. In der Realität gilt das aber nicht. Die Bündelung ist nur mit einer parabolischen (asphärischen) Fläche ideal, und asphärische Linsen sind komplizierter und teurer in der Fertigung. Zudem ist die Brechung von der Farbe des Lichtes (der Wellenlänge) abhängig, und die Wellennatur des Lichtes vergrößert den Durchmesser des Bildpunktes (Stichwort Beugung). Ein Objektiv schafft es also nicht, die Lichtstrahlen auf einen im Idealfall unendlich kleinen Punkt zu bündeln, was zu einer Begrenzung der Schärfeleistung führt.  Wie stark diese Begrenzung ausfällt, hängt von der Konstruktion und damit auch meist vom Preis des Objektivs ab. Hinzu kommt der Einfluss der Schärfentiefe. Rückt ein Punkt im Objekt näher an die Linse heran, so wandert der Bildpunkt weiter nach hinten. Um dieses Wandern auszugleichen, kann ein Teil des Objektivs bewegt werden. Es wird fokussiert. Dabei wird eine bestimmte Ebene (alle Punkte mit gleichem Abstand zum Objektiv) scharf abgebildet. Punkte davor oder dahinter werden mehr oder weniger unscharf, doch ab wann ist die Unschärfe sichtbar. Die entscheidende Frage lautet also: Ab wann ist ein Objekt unscharf? Ist das der Fall, wenn das Strahlenbündel in der Fokusebene, der sogenannte Unschärfekreisdurchmesser (u'), größer ist als 1 Pixel?

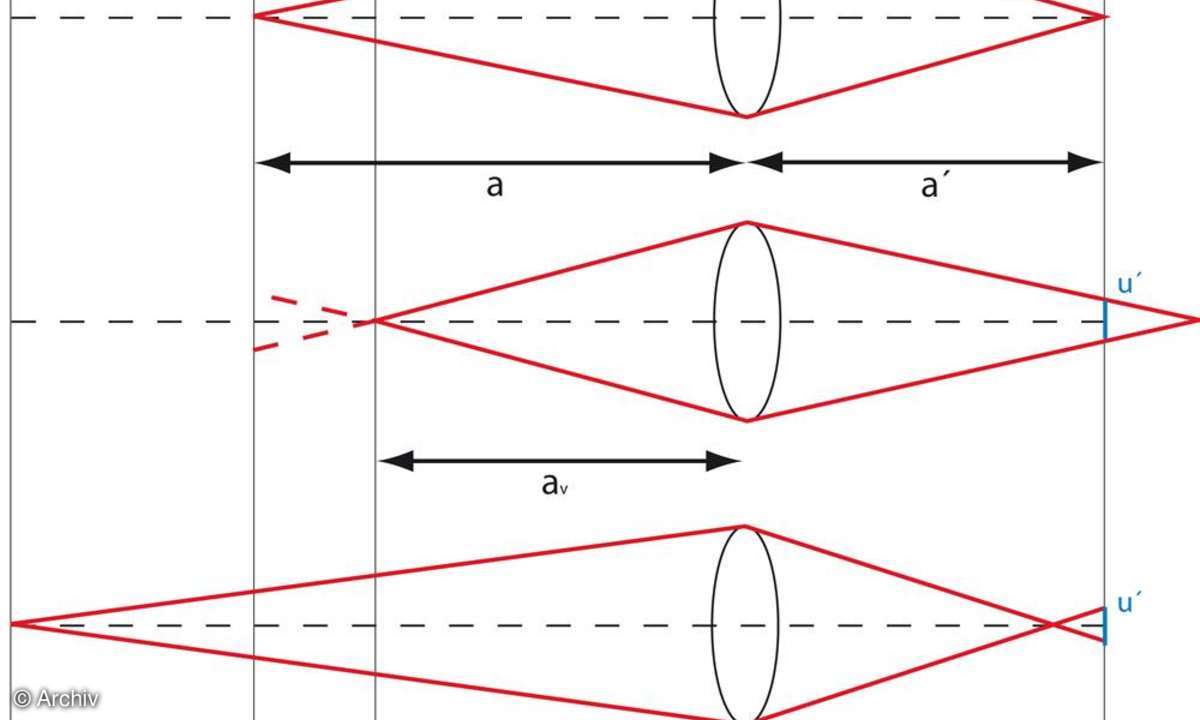
Schärfentiefe - der konventionelle Ansatz

Grundsätzlich lässt sich die Frage so beantworten, dass ein Objekt dann unscharf ist, wenn man mit dem Auge den Kontrast- bzw. Detailverlust erkennen kann. Wann das der Fall ist, hängt von den Betrachtungsbedingungen, also der Größe des Bildes und dem Betrachtungsabstand ab. Ein Bild im Postkartenformat wird eher als scharf gelten als ein Poster, das man aus kurzer Distanz betrachtet. Wird das Poster aber von der gegenüberliegenden Straßenseite aus betrachtet, so wird es dem Auge auch wieder scharf erscheinen. In der klassischen Fotografie ist man davon ausgegangen, dass eine typische Betrachtungsbedingung das Bild  im Format 10 x 15 cm ist, das aus 25 cm Entfernung betrachtet wird. Wird ein Bild größer ausgegeben, so wird üblicherweise auch die Betrachtungsentfernung vergrößert, was unter dem Strich zum gleichen Schärfeeindruck führt.

Geht man davon aus, dass das menschliche Auge Details erkennen kann, die etwa 2 Bogenminuten auseinander liegen, so entspricht das bei einer Betrachtung aus 25 cm Entfernung einem Abstand von 0,14 mm zwischen zwei Linien. Enger zusammenliegende Linien sind unter den klassischen Betrachtungsbedingungen nicht erkennbar. Da das Negativ aber etwa viermal kleiner ist, als der 10 x 15-cm-Abzug, darf der Abstand in Negativ lediglich 0,033 mm betragen.

Werden die gleichen Überlegungen auf die digitale Fotografie angewendet, so ergibt sich eine notwendige Nachvergrößerung des Bildes aus der Sensorebene, die von der Sensorgröße abhängt. Die Größe des zulässigen Unschärfekreisdurchmessers (u') muss deshalb durch den Brennweitenfaktor, der zur Berechnung der äquivalenten Kleinbildbrennweite verwendet wird, geteilt werden und ergibt den zulässigen Unschärfekreisdurchmessers für die spezifische Kamera.

Einige Beispiele:\xe2\x80\xa2 Der APS-C-Sensor einer digitalen Einsteiger-SLR-Kamera besitzt einen Faktor von 1,5. => u'= 0,033 / 1,5 = 0,022 mm\xe2\x80\xa2 Der 1/2,5-Zoll-Sensor einer kompakten Digitalkamera besitzt einen Faktor von 6,4. => u' = 0,033 / 6,4 = 0,0052 mm 

Die diversen Programme, die einem die Schärfentiefe berechnen können, verwenden genau diesen Ansatz. Da aber die meisten Anwender die Brennweitenfaktoren nicht auswendig wissen, sind häufig die Digitalkameratypen auswählbar. Hier ein paar Internetseiten, auf denen sich Schärfentiefe-Rechner finden, die online benutzt oder heruntergeladen werden können:https://www.dofmaster.com/dofjs.htmlhttps://www.photografieren.de

$umbruch$

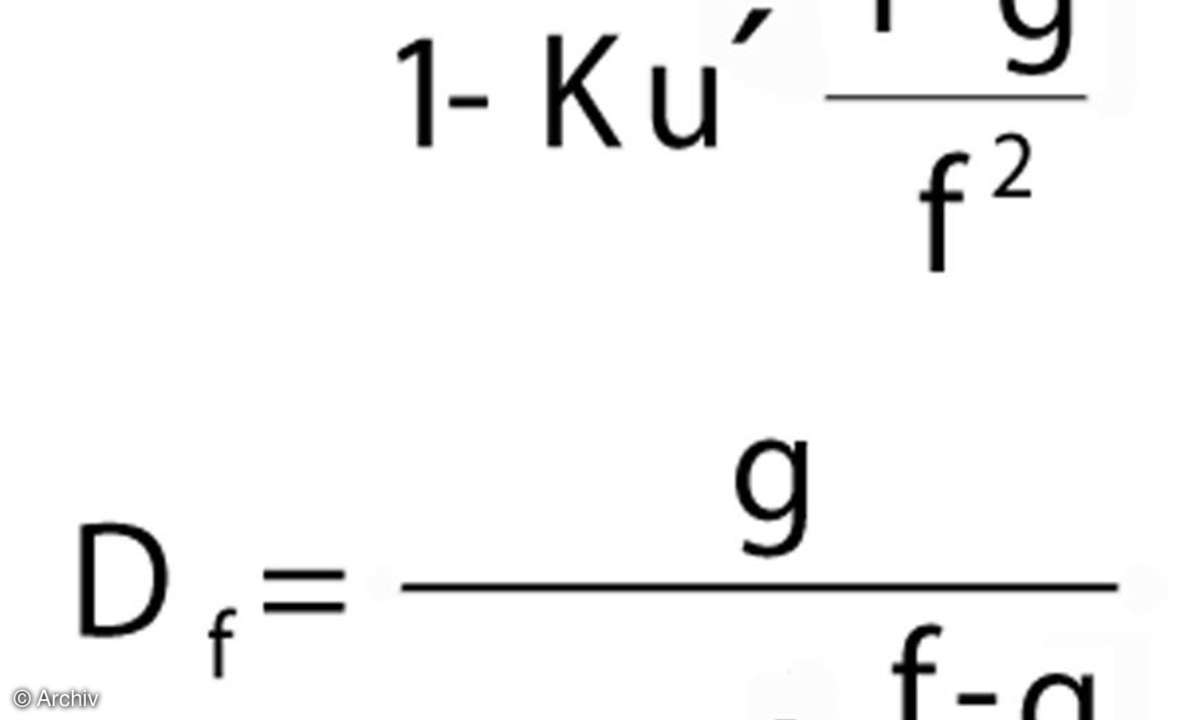
Schärfentiefe - Formeln zur Berechnung

Wer sich die Schärfentiefe selber ausrechnen möchte, kann die folgenden Formeln verwenden: Benötigt werden:f: die Brennweite in mm (nicht die äquivalente Kleinbildbrennweite!)g: die eingestellte Aufnahmeentfernung in mmDn: vordere Grenze des scharfen Bereichs in mmDf: hintere Grenze des scharfen Bereichs in mmK: Blendenzahl    u': der Unschärfekreisdurchmesser in mm

$umbruch$Schärfentiefe - die ultimative Schärfe

Der klassische Ansatz geht also von der 10 x 15-cm-Vergrößerung aus, die aus 25 cm Entfernung betrachtet wird. Was aber, wenn das Bild in der 100%-Darstellung auf dem Monitor angezeigt wird? Die Auflösung der heutigen Monitore beträgt üblicherweise 96 ppi, was einer Pixelgröße von 0,26 mm entspricht. Da - wie das Nyquist-Theorem besagt - wir immer 2 Pixel brauchen, um eine definierte Struktur darzustellen, ist der darstellbare Unschärfekreis 0,52 mm groß. Im Gegensatz zur Betrachtungsentfernung des 10 x 15-cm-Bildes werden Monitore aber aus etwa 50 cm Entfernung betrachtet. Das bedeutet, dass wir auf einem Monitor eine um etwa den Faktor 2 schlechtere Detailwiedergabe haben, als das menschliche Auge theoretisch sehen könnte. Dazu wird das einzelne Pixel auf 0,26 mm vergrößert. Die Stärke der Nachvergrößerung und damit auch der Vergrößerung des Unschärfekreisdurchmessers hängt also von der Pixelgröße auf der Sensorebene ab. Der zulässige Unschärfekreisdurchmesser für diese Art der Darstellung berechnet sich nach:

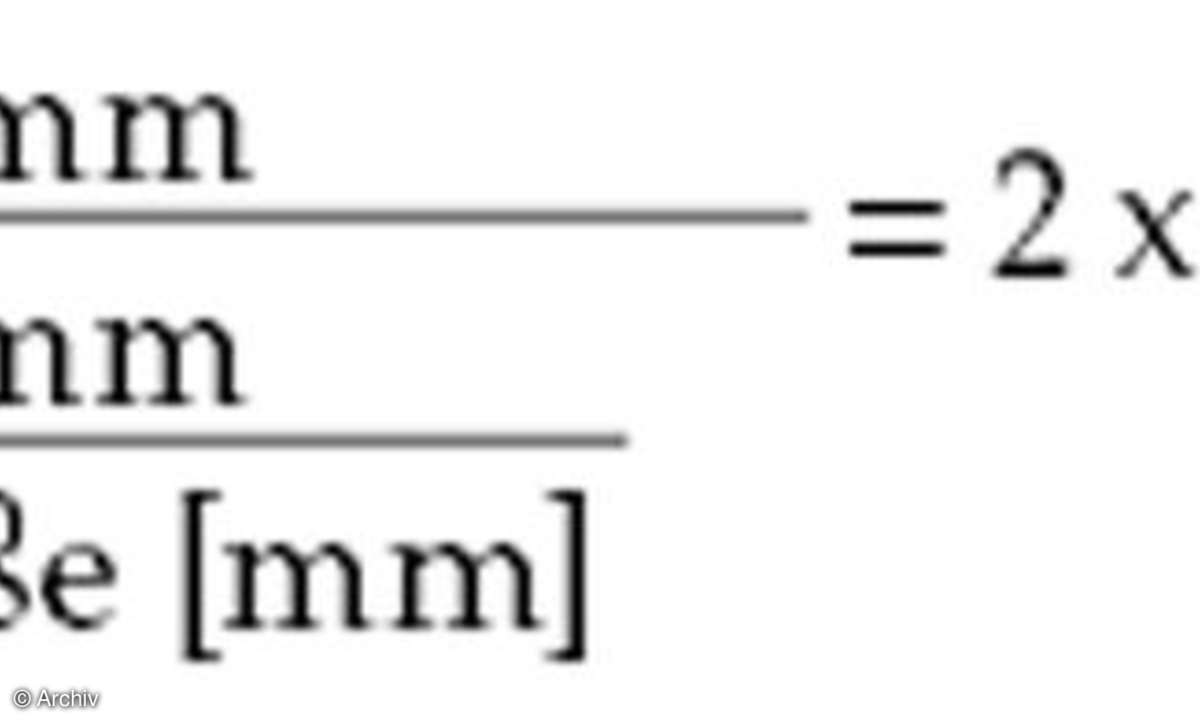
Bei dieser ultimativen Betrachtung führt eine höhere Auflösung zu kleineren Pixeln, einem kleineren Unschärfekreis und damit einer sinkenden Schärfentiefe. Allerdings ist die Betrachtung durch die 100%-Darstellung damit nicht mehr absolut.

Vergleich der konventionellen mit der ultimativen Methode

Eine Vergleichsrechnung: Pentax K20D: Brennweitenfaktor: 1,54; Pixelpitch: 0,005 mm; Brennweite: 30 mm; Aufnahmeentfernung: 3 m; Blende: 4u' konventionell =  0,033 / 1,54  = 0,022 mmu' ultimativ = 2 x 0,005 mm = 0,010 mm